Действия
со степенями
со степенями






Аудиозапись по теме
Определение
натуральной степени числа
натуральной степени числа
1.1
Сегодня мы поговорим о степенях и о действиях со степенями и дадим определение того, что такое степень, а затем все свойства, правила и действия, которые из этого определения последуют.
Начнем с определения натуральной степени



Правило
Натуральной степенью числа a называется само это число, взятое n раз, и умноженное само на себя.
an = a × a × ... × a
n штук
Число а при этом называют основанием, а число n — показателем степени.

Частные случаи
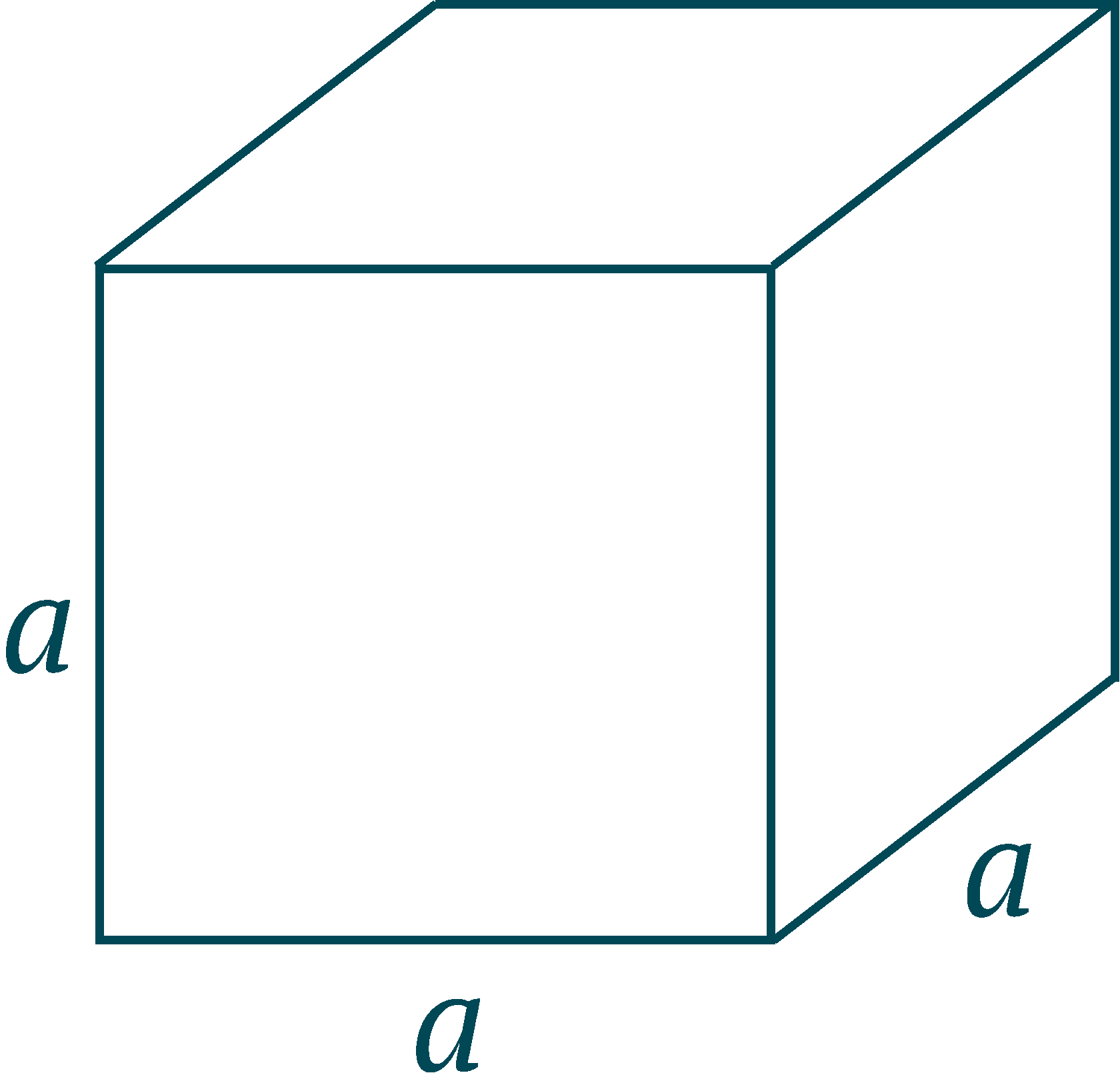
Это a2, «a в квадрате», потому что это площадь квадрата со стороной a.
Есть ещё «a в кубе» — a3, это соответственно объем куба со стороной a.
a × a × a = a3

a × a = a2
Основные свойства степеней
1.2
Оказывается, довольно много.
an × am = a × a ×... × a × a × ... × a = an + m
Наверное, очевидно, что их надо сложить.
Первое свойство


n штук
m штук


+
Например, вот такое первое свойство:
И что же мы из этого определения можем получить?
Правило
При умножении одинаковых оснований в каких-то степенях этих степеней складываются.
an
Допустим, что мы хотим поделить an на am.
Мы рассмотрим сейчас случай, когда у нас n > m.
Мы рассмотрим сейчас случай, когда у нас n > m.
am
=
a × a ×... × a × a × a
a × a ×... × a
= an – m


n штук
m штук
Второе свойство


Правило
При делении степеней с одинаковыми основаниями показатели степеней вычитаются.
Дальше мы рассмотрим:
( an )m = an × an ×... × an = an × m
Для большей наглядности можно каждую an расписать по определению:
( an )m = a × a ×... × a
a × a ×... × a
a × a ×... × a
...
Подсчитав все элементы этой таблицы, мы получим an × m, что и подтверждает третье свойство.
Поскольку сам принцип подсчета площади фигуры и состоит в том, чтобы просуммировать все единицы (элементы единичной площади), которые удается уложить в данную фигуру.
Заметьте, что число элементов в нашей таблице мы вычислили по сути по формуле площади прямоугольника — это не случайно.

m штук

n

n

m



Третье свойство
Правило
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
Мы помним, если числитель равен знаменателю, то это всегда единица:
Дальше мы рассмотрим случай второго свойства, при котором уже n = m.
Но по второму свойству:
an
am
am
am
=
= 1
am
am
= am – m = a0
Определение нулевой и отрицательной степени

Значит, при n=m
Правило
Какое бы число (кроме нуля) ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Четвертое свойство
a0 = 1
Действуя примерно таким же образом, мы можем
Таким образом, получим пятое свойство.
a– m
По второму свойству:
a– m = a0 – m =
a0
am
1
am
=
рассмотреть теперь такой случай:
Пятое свойство
Правило
Число a в отрицательной степени — это единица, деленная на число a в натуральной степени:
a–m =
am
1
Можем рассмотреть теперь произведение чисел с разными основаниями и одинаковыми степенями:
Опять-таки расписываем всё это по определению:
an × bn =
Мы знаем, что умножение ассоциативно и коммутативно, то есть порядок не важен. Значит a и b, поскольку их одинаковое количество, можно переставить местами:
А это собираем обратно по определению: = (ab) n
= a × a × ... × a × b × b × ... × b =


n штук
n штук
= (ab) × (ab) × ... × (ab) =

n штук





Шестое свойство
Если в произведении степенией основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.
an × bn = (ab)n
Нетрудно догадаться, что тоже самое произойдет с делением.

Предлагаем провести доказательство самостоятельно.

Седьмое свойство

Правило
Если при делении степеней основания разные, а показатели одинаковые, то нужно возводить в степень частное оснований.
bn
an
a
b
=
(
)
n
Эти свойства основные. На этом, как правило, действия со степенями заканчиваются. Но мы можем немножко ещё порассуждать и прийти таким же естественным образом к понятию корня — как квадратного, так и произвольной натуральной n-ой степени.
Вывод



Корень n-ой степени числа. Дробная степень.
1.3
Еще раз запишем определение дроби

n штук
an
= a × a × ... × a
и семь рассмотренных свойств:
an × am = an+m
an
am
= an–m, n > m
1)
2)
3)
4)
5)
6)
7)
(an)m = an×m
a0 = 1
a–n =
an
1
an × bn = (ab)n
an
bn
=
(
)
n
a
b
def


В заключение введем определение:
n
a = b такое, что bn = a
Мы видим, что
4 = 2, потому что 22 = 4.
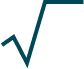
9 = 3, потому что 32 = 9.
Или
Это и есть примеры вышеприведенного определения.
Но здесь важно сказать, что при четных степенях возникает неоднозначность.
Поэтому, чтобы избавиться от неопределенности, договариваются рассматривать только положительные значения.
(–2)2 = 4
(–3)2 = 9
Например:
То есть в наших примерах это +2 и +3.



Если
Поскольку основания здесь одинаковые, то нам просто нужно подобрать такой х, который при умножении на n, давал бы нам 1, то есть первую степень числа а, ну или просто само а.

n
a = b
то из введенного выше определения следует, что

a
= a1
)
n
(
Допустим, что нам не нравятся все эти корни и скобки, мы хотим записать этот пример по-другому — как тоже какую-то степень числа а:
(ax)n = a1
Соответственно, мы можем решить уравнение:
nx = 1, откуда x =
1
n
Восьмое свойство
Девятое свойство
n
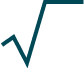
a = a
n
1
m
n
= a
n
1
am = am×
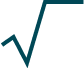
n
Таким образом, мы получили дробную степень, у которой теперь есть строго определенный смысл.
Вывод



В заключение рассмотрим такую задачу
Заключение
Доказать, что
То есть, нам предлагается убедиться, что степень «затаскивается» под корень.
Задача хороша тем, что здесь появляется так называемая «чистая алгебра» — манипуляция абстрактными символами по определенным нами заранее правилам.
n
a )m
(

=

n
am






Давайте вместе разберем, как она решается
Возможно, что вы разделите этот «умеренный» восторг с нами.
Что нужно сделать чтобы это доказать?
Давайте применим свойство (8) и запишем:.
Как мы помним, по правилу действий со степенями:
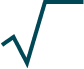
n
a )m =
(
1
n
(
a
)
m
(a
1
n
)
m
= a
m
n
Далее просто поменяем местами m и n, и, применив на этот раз тождество (9), получим:
a
m
n
=
(am)
1
n
=
n
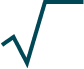
am









Еще раз обращаем ваше внимание на то, что все операции со степенями совершенно естественным образом были получены из исходно принятого нами же самими определения — в этом суть и свобода математики!
Вывод



Журнал развивается и регулярно пополняется новыми материалами.





x + 1
x, y
010100
Подписывайтесь и знакомьтесь с ними первыми!